Making simple 4D maps

Making simple 4D maps
I want to show you some ways to represent puzzles with four spatial dimensions. Even though the fourth dimension is used to make the puzzles more exciting, 4D puzzles can show the simplicity of adding one dimension. Playing these puzzles helps visualizing more dimensions than the three we notice in day-to-day life.
Dimensions
If you don't look too closely, a grain of sand is a 0D object, a thread 1D, a piece of paper 2D, and a block of wood 3D.
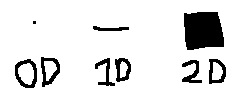
In a 1D world you can only move forward and backward, in 2D you can also move left and right. Moving diagonally is a combination of the others, so doesn't count as a new direction. In 3D you can also go up and down, and for 4D we add two more directions.
To check the number of dimensions of space, get as many sticks as possible perpendicular to each other (as seen here). You get to three in this universe, if your sticks aren't too fancy.
Projections
What's the use of talking about four dimensions in a 3D world? The same as talking about 3D games or any other seemingly 3D thing on your 2D computer screen, TV, canvas or paper. Things can feel 3D or 4D, even though the final product is 2D. Squashing an object to lower dimensions, like taking a picture or making a shadow on a wall, is called projection. You can always project, project, project, all the way down to zero dimensions. Here is a projection of a ball:

and here's the projection from the top of that projection:
Slices
Our human eyes use projections, but wouldn't it be nicer to be more alien and look at things like an MRI-scanner? Instead of having your vision blocked by the surface of objects, let's slice them up so you can look inside them. You have to choose how thinly you want to slice things. More slices means there is less space per slice in your field of vision, but less slices means you might miss things in between your slices. Here is the sliced up ball, which turns out to have an orange inside:

Pre-chopped space
Games are easier to slice up if the playing field is made of separate squares, like chess or checkers, where you jump between places. (These are technically 1D, but the 2D description is simpler.) You can then give each square a name or number:
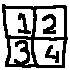 ,
,
which can be sliced up like this: .
.
The left square in the left slice is next to the left square in the right slice, so 1 is still next to 2 and 3; 2 is still next to 1 and 4, etc. This doesn't accomplish much, but now we have room for a third dimension on our 2D screen: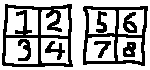 ,
,
where 1 is now next to 2, 3 and 5. 7 is next to 5, 8 and 3. To get to 4D, we can also put slices vertically: .
.
Now 1 has four neighbors: 2, 3, 5 and 9, because 5 and 9 are in the same position in adjacent slices. This is like putting two cubes next to each other, and acting like the same positions inside the two cubes are adjacent.
Mazes
The most basic way to explore a 4D space is to just walk around. To make the walking around a little bit more interesting, people make mazes.
Some examples
Going on a quest to find examples of 4D mazes and puzzles leads you through some great old-school web pages like http://www.astrolog.org/labyrnth.htm. There are multiple people who seemingly made it their life's work to collect information about 4D things and mazes. A handy start is https://en.wikipedia.org/wiki/List_of_four-dimensional_games.
Different types of representations are in that list. First, there's the projection of higher dimensional things on a 2D screen seen in http://superliminal.com/cube/cube.htm.
Then there's the option of taking a 3D slice of a 4D world: https://www.youtube.com/watch?v=0t4aKJuKP0Q. The maker of that video, Marc ten Bosch, has done a lot of work in this field, and is now working on Miegakure. Miegakure stands out because it's more polished than other 4D games, and you can smoothly walk around, instead of step by step.
Finally, instead of slicing just once, you can use the 2D grid of 2D slices we've seen before. This 4D crossword puzzle is a simple example: http://www.ing.iac.es/~crb/misc/xwd65.html, and there's more to be found here: http://old.nklein.com/products/54321/. Here's a 2x2x2x2 solved crossword:
 .
.
Notice words like ai (a type of sloth), ti and no. (aa is rough lava. This list of 2-letter words was helpful.)
Triangles and big wally squares
If you want to have a clear overview of a 4D maze, this 2D grid of 2D slices is often used. There are two ways these mazes are represented: Spaces with lines in between, or having walls and open squares take up the same amount of space. The first one seems more natural for drawing mazes: you take a blank piece of paper and draw walls on it using your pen lines. The second one is like using graph paper and coloring in squares for walls. 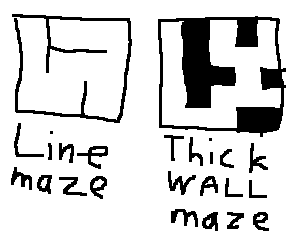
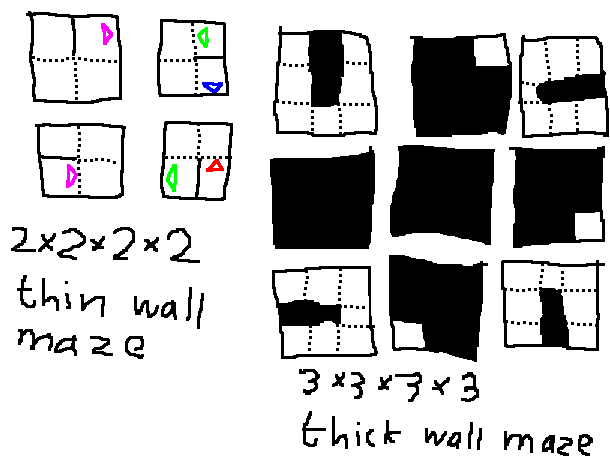
To walk around in 4D, the thin wall system needs to show possible moves between slices. Usually triangles point in the direction of the square to jump to (like here). In the next picture, the way from 1 to 3 is blocked, but 2 has a triangle pointing to the right, so you can reach 4 from there. The triangle to the left in 4 also allows to go back to 2 from 4. (Everybody colors these triangles, so I do too.)

The thick wall maze expands more naturally to four dimensions when using 2D slices. With square walls, you can move to the same position on adjacent squares. To show a passage, you can show an absent wall on the next slice. This is the system used in Boxpusher 4D.
In these examples you can follow the same route from the top left all the way through the maze:
 .
.
Here is the route:
 .
.
With thin walls, you need a lot of triangles for a big empty room. Thick walls are thus better for games which have more open spaces:

Thick wall games also feel less like you're teleporting, although that still is an issue in getting that 4D feeling.
Making it feel 4D
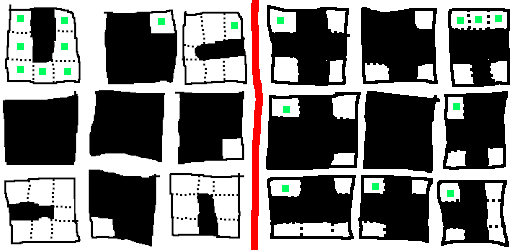
Letting things feel 4D instead of some weird thing where you teleport around is quite challenging. One thing that helps is switching dimensions around to show that you get the same puzzle in a different view. Here is the same maze as before to the left, and on the right a version with the dimensions switched:
 .
.
On the right, the first six steps are still in a U-shape, but now you jump between slices. Next, where in the left maze you jump two slices to the right, in the right maze there are two little steps. The same steps in both mazes are shown in green.
Something else that works well is when you can't see everything on your screen at once, like with a 10x10x10x10 map on a 4x4x4x4 grid, and you scroll in different directions.
6D? 20D?
Yes, you can expand this approach to n dimensions. You do need enough screen space. And it probably gets confusing.
Get Boxpusher 4D
Boxpusher 4D
Finally some 4D box pushing!
| Status | In development |
| Author | trudieprod |
| Genre | Puzzle |
| Tags | 4d |

Leave a comment
Log in with itch.io to leave a comment.